Game of Life

    for each cell

        count = 0

        for each neighbor

            if currentState == alive

                count = ++

        if count == 3

            nextState = alive

        else if count != 2 or 3

            nextState = dead

I’m starting with a straightforward, ‘naive’ implementation in Python just to get something up and running. Of course nothing is ever as simple as the pseudo-code so there are a number of functions necessary to set everything up, run the algorithm and display the results.

First things first…let’s make some declarations about the nature of the universe:

#Declarations
rows = 40       #num rows of matrix
columns = 80    #num columns of matrix
fps = 20        #number of frames per second to display
cycles = 500    #number of simulation iterations
use_seed = 1    #0=no, 1=yes
#define locations of 8 neighbor cells
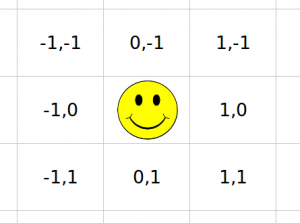
neighbors = [[-1,-1],[0,-1],[1,-1],[-1,0],[1,0],[-1,1],[0,1],[1,1]]

seed = [[0,0,1],   #glider
        [1,0,1],
        [0,1,1]]
#seed =  [[0,1,0],   #blinker
#         [0,1,0],
#         [0,1,0]]

 This defines a grid that is 40 rows by 80 columns and is updated 20 times per second for 500 cycles. The interesting part here is the definition of the neighbors which defines the way the grid is connected. Each cell has eight neighbors with the relationship to the cell as shown below. Defining the neighbors in a list makes it easy to iterate over them later.

I’ve also defined a couple of starter patterns (seeds) that I can use just to make sure everything is working. The blinker alternates between horizontal and vertical and the glider glides. Now it’s time to initialize the grid with living and dead cells:

#Initialize
currentState = populate(rows, columns, use_seed, 3, 3, seed)

which calls the populate function:

def populate(numR, numC, use_seed, insertR, insertC, seed):
    #populate either with a seed or with random 1s and 0s
    if use_seed == 0:
        #Populate with random field of 1s and 0s
        currentState = [[random.randint(0,1) for i in range(numC)] for j in range(numR)]
    else:
        #Populate with seed
        currentState = [[0 for i in range(numC)] for j in range(numR)]
        nextState = [[0 for i in range(numC)] for j in range(numR)]
        Cseed = len(seed[0])
        Rseed = len(seed)
        for i in range(Rseed):
            for j in range(Cseed):
                currentState[insertR+i][insertC+j] = seed[i][j]
    return currentState

This function either places the predefined seed into the grid or fills it with a random set of living and dead cells.

We then get into the main loop which calls the code that actually runs the GOL algorithm and then displays the results:

#Main
print "Running"
for i in range(cycles):
    currentState = update_state(currentState, neighbors)
    #print "Cycle ", i
    display(currentState,fps)
print "Done"

I’ve included the pseudo-code algorithm in the update_state function as a reminder to myself later when I go back and look at this.

def update_state(currentState, neighbors):
    '''
    this function is where the actual game of life calculations happen    
    for each cell
        count = 0
        for each neighbor
            if currentState == alive
                count = ++
        if count == 3
            nextState = alive
        else if count != 2 or 3
            nextState = dead
    '''
    nextState = copy.deepcopy(currentState)
    Rindex = 0
    for row in currentState:
        Cindex = 0
        for cell in row:
            count = 0
            for neighbor in neighbors:
                # % does modulo indexing to create toroidal universe
                neighborR = (Rindex + neighbor[1]) % len(currentState)
                neighborC = (Cindex + neighbor[0]) % len(currentState[0])
                if currentState[neighborR][neighborC] == 1:
                    count += 1
            if count == 3:
                nextState[Rindex][Cindex] = 1
            elif count != (2 or 3):
                nextState[Rindex][Cindex] = 0
            Cindex += 1
        Rindex += 1
    return nextState

Like the code says…this basically just iterates over the cells, counts the number of living neighbors each cell has and sets its state according to the rules.  I’m just using Python lists here and iterating over each item in the list so this isn’t the fastest way to do it. I plan to switch over to a NumPy and SciPy implementation later though to speed it up. For now though this is straightforward, easy and best of all…works. The indexing of the neighbor cells is done using modulo math which turns the grid into a toroid so that when it reaches the edge it doesn’t just fall off. Instead it reaches back around to the other side and looks at the cells there.

So now that we have our updated population of cells how do we see the results? For the work so far I’ve just been using Vim and terminal windows in Linux as my development environment. While this doesn’t have much going for it in the way of fancy graphics it does make it easy for me to work locally, transfer my code to the Amazon computers and run the code there as well. So, I wanted a way to display the results of each iteration in a terminal window without a lot of fuss. The display function below does just that:

def display(universe, fps):
#very simple routine to display animated cell state in terminal
    #calculate time to sleep
    sleepTime = 1.0/fps   				
    #clear screen and reposition cursor
    sys.stderr.write("\x1b[2J\x1b[H")   
    for row in universe:
        for column in row:
            if column == 0:
                #leave empty for 0
                sys.stdout.write(' ') 
            else: 
                #fill in for 1
                sys.stdout.write('#')  
        print "\r"
    sys.stdout.flush()
    time.sleep(sleepTime)

Essentially this just takes the current state values and goes through printing characters to the screen…a blank for a 0 and # for a 1. It then goes to sleep for a bit before returning so that the display is updated at the fps rate. This line does just what it says:

    sys.stderr.write("\x1b[2J\x1b[H")   #clear screen and reposition cursor

That way we have a smooth animation of the activity rather than a scrolling mess of printouts. Of course the resolution isn’t great…this is ASCII art after all…but it suffices for making sure everything is working as it should.

Complete Game of Life code listing:

# vim: tabstop=8 expandtab shiftwidth=4 softtabstop=4

'''
Chad Bonner Nov.23.2013
Game of Life

'''
#Module import
import copy
import sys
import time
import random

# Function Definitions

def update_state(currentState, neighbors):
    '''
    this function is where the actual game of life calculations happen    
    for each cell
        count = 0
        for each neighbor
            if currentState == alive
                count = ++
        if count == 3
            nextState = alive
        else if count != 2 or 3
            nextState = dead
    '''
    nextState = copy.deepcopy(currentState)
    Rindex = 0
    for row in currentState:
        Cindex = 0
        for cell in row:
            count = 0
            for neighbor in neighbors:
                # % does modulo indexing to create toroidal universe
                neighborR = (Rindex + neighbor[1]) % len(currentState)
                neighborC = (Cindex + neighbor[0]) % len(currentState[0])
                if currentState[neighborR][neighborC] == 1:
                    count += 1
            if count == 3:
                nextState[Rindex][Cindex] = 1
            elif count != (2 or 3):
                nextState[Rindex][Cindex] = 0
            Cindex += 1
        Rindex += 1
    return nextState

def display(universe, fps):
#very simple routine to display animated cell state in terminal
    #calculate time to sleep
    sleepTime = 1.0/fps   				
    #clear screen and reposition cursor
    sys.stderr.write("\x1b[2J\x1b[H")   
    for row in universe:
        for column in row:
            if column == 0:
                #leave empty for 0
                sys.stdout.write(' ') 
            else: 
                #fill in for 1
                sys.stdout.write('#')  
        print "\r"
    sys.stdout.flush()
    time.sleep(sleepTime)

def populate(numR, numC, use_seed, insertR, insertC, seed):
    #populate either with a seed or with random 1s and 0s
    if use_seed == 0:
        #Populate with random field of 1s and 0s
        currentState = [[random.randint(0,1) for i in range(numC)] for j in range(numR)]
    else:
        #Populate with seed
        currentState = [[0 for i in range(numC)] for j in range(numR)]
        nextState = [[0 for i in range(numC)] for j in range(numR)]
        Cseed = len(seed[0])
        Rseed = len(seed)
        for i in range(Rseed):
            for j in range(Cseed):
                currentState[insertR+i][insertC+j] = seed[i][j]
    return currentState

#Declarations
rows = 40       #num rows of matrix
columns = 80    #num columns of matrix
fps = 1       #number of frames per second to display
cycles = 500    #number of simulation iterations
use_seed = 0	#0=no, 1=yes
#define locations of 8 neighbor cells
neighbors = [[-1,-1],[0,-1],[1,-1],[-1,0],[1,0],[-1,1],[0,1],[1,1]] 

seed = [[0,0,1],   #glider
        [1,0,1],
        [0,1,1]]
#seed =  [[0,1,0],   #blinker
#         [0,1,0],
#         [0,1,0]]

#Initialize
currentState = populate(rows, columns, use_seed, 3, 3, seed) 

#Main
print "Running"
for i in range(cycles):
    currentState = update_state(currentState, neighbors)
    #print "Cycle ", i
    display(currentState,fps)
print "Done"